Three Register Inversion Paper

Here is an idea for a paper: In an elliptic curve processor like mine (which has dedicated squaring and needs one dedicated register to hold a multiplier partial product) Itoh-Tsujii inversion takes 4 registers total, but it can be done in only 3 registers. The final operation of the encryption process is the conversion from projective to affine coordinates that requires dividing the final two numbers. That is the only division required. My current solution needs a total of 5 registers: 1 to hold the numerator while the denominator is inverted in the other 4 registers. Then numerator and inverted denominator are multiplied together. If I want to get my processor down to 4 registers total, I need to do inversion in 3 registers.

Doing inversion is 3 registers instead of 4 is a simple idea, but maybe it's not obvious. The simple idea is buried under several layers of detail, and the idea can be compared to others in terms of execution time, so maybe it's worth a paper.

To understand the idea, there are several layers to understand:

Elliptic Curve Cryptography in GF(2^m)
Fermat's Little Theorem
GF(2^m) Exponentiation
The Itoh-Tsujii algorithm
Combining Integers

Elliptic Curve Cryptography in GF(2^m)

The only important thing here regarding elliptic curve cryptography in GF(2^m) is that m must prime. If m were composite it would be weaker, weaker certainly than the next smaller number that is prime, so m is always chosen to be prime. A typical number for m is 163.

Fermat's Little Theorem

The theorem says that a^q = a (mod q), which says that raising a to the power q, modulo q, will give a. In the binary extension Galois field, GF(2^m), where values are represented by a vector of m bits, q = 2^m. So raising a to the power 2^m gives the original number: a^q = a. And if we multiply both sides by a^-2, we get a^q-2 = a^-1, which is the inverse of a. So we can get the inverse by raising to the power 2^m - 2.

GF(2^m) Exponentiation

With a dedicated squarer, squaring is a combinatorial circuit and is as cheap as addition. Multiplying is relatively expensive, having the same area as addition but requiring O(m) time. Using a dedicated squarer and multiplier requires one register for the multiplier partial product. Operands can be read directly out of registers. No temporary registers inside the multiplier are needed for operands.

To perform exponentiation, we can perform operations on a particular base number, raised to various powers. Squaring has the effect of doubling the exponent, shifting the exponent to the left by one bit. Multiplying two numbers that are exponentiations of the same base has the effect of adding the exponents. So an algorithm to raise a GF(2^m) number to the power 2^m - 2 using squaring and multiplying is the same as an algorithm for forming the number 2^m - 2 by shifting and adding.

Itoh-Tsujii Algorithm

The interesting thing about this algorithm is to look at 2^m - 2 in binary. For example, if m = 5, then 2^m - 2 in binary is 11110. In fact, 2^m - 1 in binary is m one bits, and 2^m - 2 = 2 × (2^m-1 - 1). If we raise a number to the power 2^m-1 - 1, then we can square it one more time and get the power 2^m - 2. So first we need to raise it to the power that in binary has m-1 one bits.

The insight of the Itoh-Tsujii algorithm, though I don't know if they thought of it first, is in raising to a power that is all one bits in binary. Their idea is if you want to get a number with double the number of one bits, shift a copy of it and add it to the original number. So if you have 1111 and want to get 11111111, just shift 1111 to get 11110000 and add to get 11111111. As I said before, shifting here is squaring a GF(2^m) number, and adding here is multiplying two GF(2^m) numbers. The goal is to get an exponent with m-1 one bits, then square one last time to get 2^m - 2. But m-1 isn't likely to be a power of two itself, so you can add a single "1" to the exponent by shifting the number and adding one. So to get 11111 from 1111 and 1, just shift 1111 to get 11110 and add 1 to get 11111.

This is really a double and add one algorithm on the number m-1 itself (while squaring and multiplying GF(2^m) numbers). Looking at the binary form of m-1, the number can be formed from left to right. The left-most significant bit is one, of course, then this is doubled and then optionally one is added if there is a one in the next most significant bit position of m-1. This is repeated, introducing bits of m-1 from left to right until m-1 is formed.

Combining Integers

If forming the number m-1 is the goal, the doubling and adding one algorithm, call it "dblinc," is not necessarily the most efficient algorithm.

At this level, the problem has been reduced to combining binary numbers composed of all one bits. If two numbers have i and j one bits, respectively, the combination with i + j one bits is formed by shifting the first number left by j bits and adding the second, or by shifting the second number by i bits and adding the first. Again, shifting (by one bit) is squaring in GF(2^m), and adding is multiplying in GF(2^m).

In the doubling and adding one algorithm, the "one" is the original number a¹. Doubling a number consisting of i one bits can be carried out by adding the number to a copy that has been shifting i bits, but of course that requires two registers and the original a¹ must be held in a third register. (My current processor requires two more registers: the multiplier partial product register and the numerator held in the fifth register.)

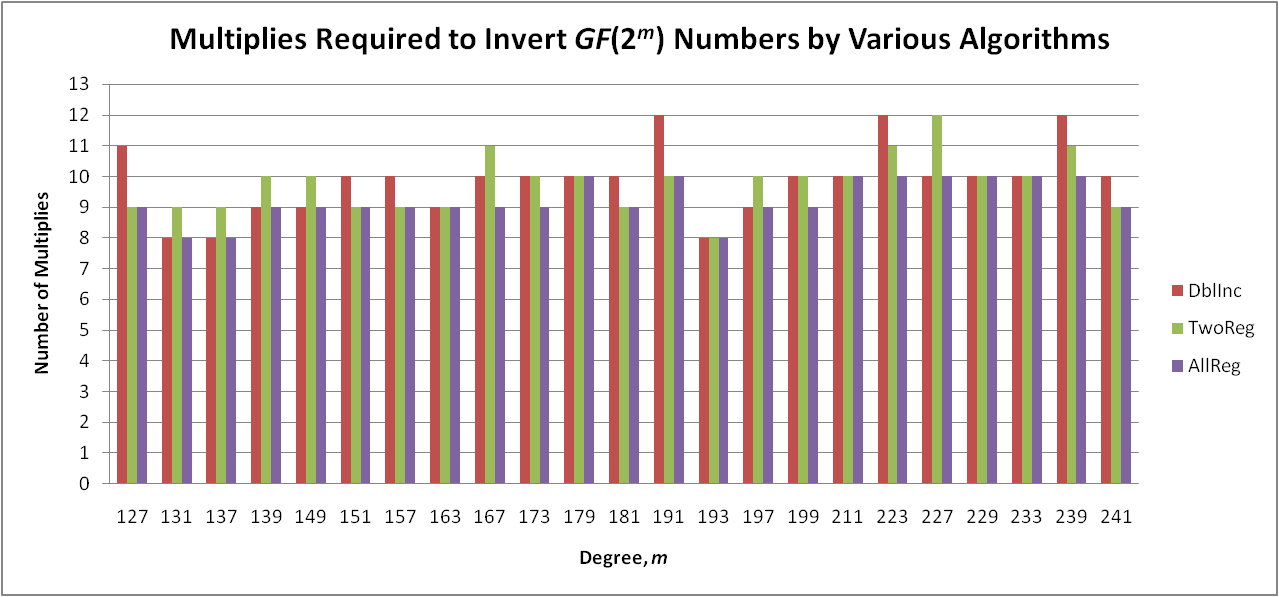
To save a register, we can use only two registers, although this method does not preserve the original a¹. This alternative design is to add two numbers with i and j one bits respectively, with the result accumulated in the multiplier partial product register. The only decision is which of the two numbers, i or j to discard and replace with i + j. The goal is still to form the number m-1. This approach, call it "tworeg" uses one less register than "dblinc". How does it compare in terms of GF(2^m) multiply and squaring operations? It turns out to be very competitive.

Since there is only one operation, adding numbers representing respective numbers of one bits, the only decisions in either of these algorithms is which results to discard to make room for the new result given a limited number of available registers. A third algorithm, call it "allreg" would have infinitely many registers, so no results would need to be discarded. 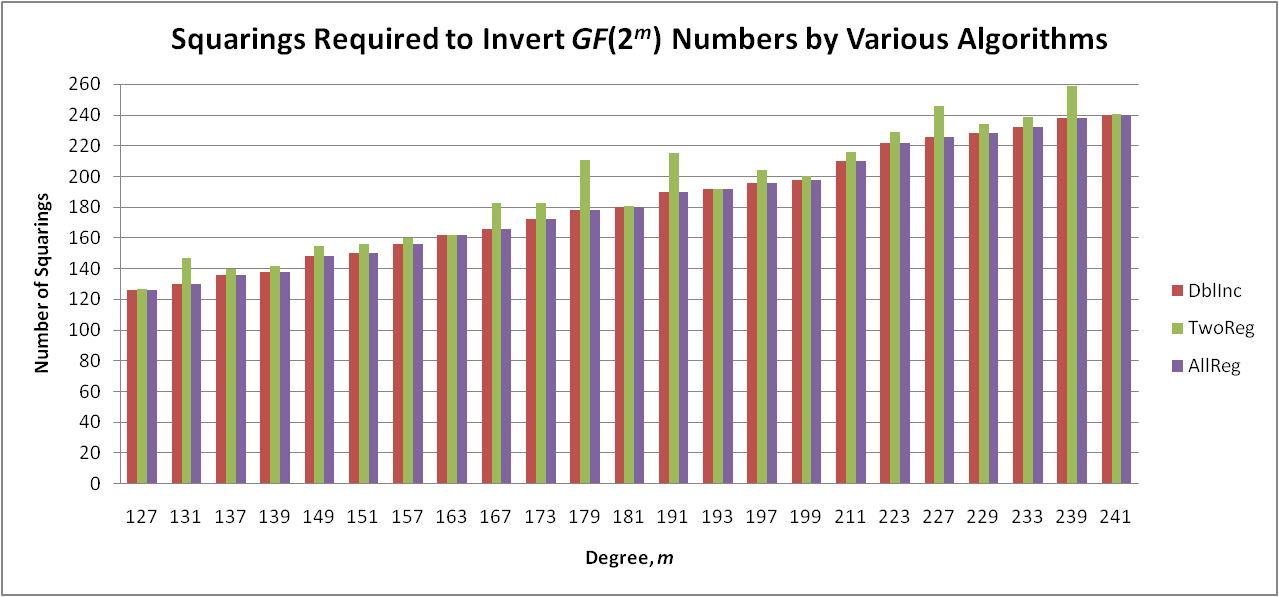This algorithm sets a lower bound on the required number of operations. A multiply requires O(m) cycles and squaring only one cycle, so these algorithms can be compared in terms of the number of multiplies and squarings, but the cost of squaring is trivial compared to multiplying.

Results

I carried out tests to compare these algorithms, although "dblincr" (which needs three registers) is the only real algorithm. To test the capabilities with two registers ("tworeg") and infinitely many registers ("allreg") I wrote programs to try all combinations and chose a combination with the minimum number of multiplies, and secondarily squarings, to invert GF(2^m) numbers for each m, the only interesting results being with m prime. Since m is a constant in these embedded processors, the steps needed can be hard-coded. The sequence of decisions needed for "tworeg" to minimize the number of operations required for an arbitrary m might be too complex to build into a small processor.

Graphs of the results are shown below. The question is: Can this be made into a paper?